The Flying Wookie: Minimal Gliding Descent

"The Flying Wookie": The Effects of Size on Minimal Gliding Descent L. Van Warren, January 1, 1996 Revised July 2, 1997

Perhaps as a result of having grown up with the movie, "Gypsy Moths", many skydivers of the "baby boomer" generation engaged in flights of fancy that had their origins in barnstorming days. In 1977, skydiver Pat Quiqley remarked , "someday people will be landing on runways with jumpsuits". His quip was an immediate response to a creative fellow who had shown up at the Fulton Missouri dropzone, looking like Chewbaka, ready to jump wearing huge furry pajamas. We watched him wookie through 1000 feet struggling to find his ripcord in the confused folds of fabric. After a long walk, and probably some soul searching he returned to the hanger with a sheepish look on his face, escorted by aviation pioneers of the past who had decided to let him live another day. Jay Weaver, the dropzone owner, rendered the obligatory safety lecture, while the rest of us rendered expressions ranging from looks of unbelief to rolling eyes. We all knew there was something to this concept, we just couldn't figure out how to do it. At the time, the Nelson brothers had a mascot that featured special little wings. The notion stuck with me to the point that when no one was looking, I built a pair and tested them by jumping on my trampoline... At this point it became clear that there were two portions to this fantasy, the recreational air portion, similar to skysurfing, and the stunt portion that wondered, "could you land this?".

At the 1993 Parachute Industry Association conference, I broached the idea of non-parachute assisted minimalist gliding to John LeBlanc, a parachute designer at Performance Designs in Florida and Tony Domenico, owner of Square-One parachute lofts in Southern California.

John LeBlanc's suggestion was to create some kind of a jumpsuit with inflatable ram-air wings. We had all seen the Krueger balloon suit slow people down to 85 mph or so, but it was a pure drag affair inflating the occupant to Michelin man freefall proportions. John wanted to build cells into the wing area under the arm. I wondered if someone could get good enough on rollerblades to land at high speeds.

At the same PIA convention,Tony Domenico suggested some kind of rigid manta-ray like shape as we sketched concepts over chicken salad in a Florida hotel.

There was something beautiful about his suggestion to look at creatures other than birds from the animal kingdom. Manta's were especially inviting, their wing spans can exceed twenty feet.

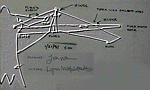Struggling with everything from condor's to cruise missles I had been imagining telescoping and "pop-out" wing designs, even an expanding oriental fan idea.

Angus Rupert had even suggested some kind of deployable rotor. In my mind I added a winglet to his idea to make it self starting. However the contrast between parachutes and a descending "pair of scissors" was too much and I abandoned that concept. The notion of an activating winglet was to remain.

I mentioned this to the distinguished aviation designer, Roy Haggard in 1995. Roy had been a player in some important aviation firsts including Jim Handbury's triple person hang-glider flight off half dome, and Dar Robinson's jump across the grand canyon, all of which used parachutes for the landing. Roy also wants to see a successful repeat of the ill-fated Snake River Canyon jump, and is one of the few people with the background and facilities to pull it off.

There have been documented incidents of landings without a parachute, but most of these have involved a combination of serendipity, trees, water, mud or several feet of snow! Thus it has been suggested by some, including the author, that some kind of sophisticated jumpsuit or minimalist glider could be developed to allow gliding descent without the use of a parachute. The real question is could any of these ever be safely landed? Consider the following fanciful story:

A plane is overhead, way up in the sky. The sound of the engine goes momentarily quiet, and three rectangular dots appear in the sky. Instead of making the usual skydiving formation these dots seem to chase the plane for a while. Soon they appear to begin manuevers, slowly twisting and tilting across the sky. Uncertain of what you've seen you look down to finish stowing the lines on your parachute, but an internal timer, refined through years of experience, is clicking in you. You look back up at what should be pull time and the dots are still small... In suspended disbelief you shake your head and return to stowing your the bagged parachute in its container with your knees. Not even an alien encounter is allowed to interupt the flow of packing... After groping for your pull-up cord you glance up again and but this time the dots are big and square, but with blurry corners. Your jaw drops as three magnificent surfers line up for final approach. In formation they are crouched with their arms out to the sides. As they descend , there are no parachutes, instead they surf like mythical figures from a suntan oil commercial. Every eye is on them in stunned disbelief. A funny whirring noise accompanies their flight. You notice that the corners of their strange square boards are vibrating up and down in a blur. With a loud horrific slide and a rat-a-tat-tat they skid to a stop, unfazed. Their feet are held by fuzzy stirrups, an out-of-place looking metal box sits at the back of their boards. It looks like a smoke detector with cables spreading outward. The corners of the board are whapping the runway asphalt, but it stops at the flick of a switch. Replacing the guard over the switch, they step off their boards, look at each other and smile. Without futher ado they heft their boards up by the stirrups and after asking for directions, ask if someone has something to eat. It takes a while for the silence to die down...

Analysis

If we assume that a stable vehicle can be constructed, and that altitude can be bled off in a manageable way, then the most important aspect of any gliding descent is the minimum velocity that can be attained. The risk of injury in a crash is directly proportional to the kinetic energy at impact. Kinetic energy is expressed as:

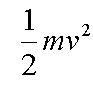
so the principal goal should be to make the landing as slow as possible. Further, at touchdown, it must be the case that the vertical component of velocity be zero. This is only possible if the lifting body or device is flying above stall speed, or is in a controlled interaction with ground effect. For the sake of this elementary analysis, I will assume that the single factor most controlling landing velocity is wing loading. Therefore we will proceed to look at the effect of wing loading in detail. But first, a quick trip to the zoo...

Several species of animals fly including squirrels, lizards and even snakes. Flying squirrels exploit special adaptations for tree to tree descent. These adaptations include skin that runs from wrist to ankle on both sides. The tail acts as a stabilizer, airbrake, and rudder. A specialized use of the tail is seen in South American snakes that engage in tree to tree flights, flying their bodies as serpentine lifting vehicles while engaging in slithering behaviors that provide stabilization. Lizards with winged body appendages and webbed feet of large relative proportion engage in gliding using their four feet as lifting and control surfaces.

Consider the flying squirrel, illustrated above. The wing loading for the squirrel in units of mass per unit area is:

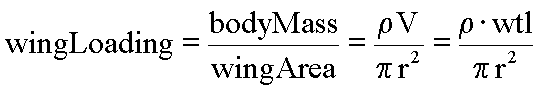
We will assume that this squirrel flies on the aerodynamic equivalent of:
1) a lifting disk whose radius r is 10 cm.
2) payload body width w of 5 cm.
3) body thickness t of 2 cm.
4) body length l of 20 cm.

We will assume that the density of the squirrel is the same as water, 1 gram per cubic centimeter. Grinding this out we get:

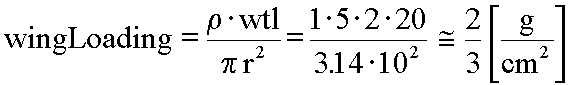
Neglecting the contribution of the tail, this works out to a wing loading of approximately 2/3 gram per square centimeter. Now we want to repeat the calculation for a "man-sized" squirrel which somehow reminds me of a wookie...

We parameterize our squirrel as follows:

1) Consider a lifting disk whose diameter is 2 r.
2) With a payload body width w = r / 2.
3) With a body thickness t = r / 5.
4) With a body length l = 2 r.

Substituting our wookie parameters into the wing loading formula yields:

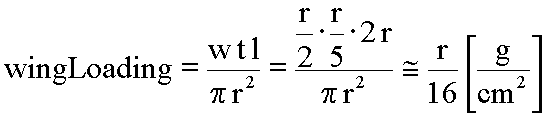
This formula, which I shall call, "The Wookie Formula", is actually quite remarkable.

It states that the "Flying Squirrel Thing" is done at a wing loading that increases linearly with animal size. It is not a constant. In ordinary terms it means, "The bigger you are, the harder you fall".

Now let's apply this to a real person six feet tall. Their radius would be 91 cm. Their "Flying Wookie" wing loading would therefore be 5.72 g/cm2, nine times the wing loading of a squirrel!. To do the "Flying Wookie" a human would have to carry nine times the surface area, or about 254 square feet. The 254 square foot area portends the the use of hang gliders and parachutes; Sports which exist and land at low speeds. Put another way, for a jumpsuit approach to work at flying squirrel speeds, the weight of a flying wookie would have to be 20 pounds, past the capability of even the most avid dieter...

Because dynamic pressure grows as the square of velocity, one could fly a vehicle with only 254/9 = 28 square feet of area if one was willing to increase flight speed by the square root of nine, or a factor of three (times faster). For typical figures this works out to about 65 mph, pretty fast for rollerblades! Pretty fast for a prone landing, but probably within reach of a clever design...